算法03贪心与动态规划
- 1. 贪心与动态规划概述
- 1.贪心
- 1.1贪心概述
- 1.2贪心常用场景
- 1.3贪心解题思路
- 2.动态规划
- 2.1动态规划概述
- 2.2动态规划常用场景
- 2.3动态规划解题模板
- 3.浅谈贪心与动态规划的关系
- 2.贪心经典题目
- 3.动态规划经典题目
- 3.1体会“从整体到局部”的思考过程
- 3.2体会“状态转移方程”系列
- (1)力扣309.买卖股票的最佳时期含冷冻期与
- (3)力扣714.买卖股票的最佳时期含手续费
- 3.3 子序列问题
- (1)
- 3.4体会什么时候用一维dp数组,什么时候使用多维dp数组
- (1)力扣718.最长重复子数组
- 3.5体会“遍历顺序”
- 体会“背包问题”
- 树形dp
- 编辑距离问题
- 4.扩展
- 优先级队列
- 大顶堆
- 参考资料:
1. 贪心与动态规划概述
1.贪心
1.1贪心概述
贪心算法(英语:greedy algorithm),又称贪婪算法,是一种在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是最好或最优的算法。比如在旅行推销员问题中,如果旅行员每次都选择最近的城市,那这就是一种贪心算法。
1.2贪心常用场景
贪心算法在有最优子结构的问题中尤为有效。最优子结构的意思是局部最优解能决定全局最优解。简单地说,问题能够分解成子问题来解决,子问题的最优解能递推到最终问题的最优解。
常用场景如下:
- 区间问题:贪心算法可以用于解决最小覆盖问题、区间选取问题等
- 小数背包问题:不同于0-1背包问题(动态规划),物品是可以分割,只装进背包一部分
- 图论中的问题:例如,Prim和Kruskal算法用于找到图的最小生成树,Dijkstra算法用于找到单源最短路径
- 与常识紧密结合的问题:分饼干、找零问题等
1.3贪心解题思路
对于贪心相关的算法题,其实没有一个比较固定的模板,常常和经验和常识有关,但这里还是做一个结构化的总结:
1.有些问题的最优解,很直观地可以想到是由一个或多个子问题“转移”而来,这时我们可以直接使用dp
2.如果一个问题我们难以从“整体”-》“局部”思考,但是可以从“局部”-》“整体”思考,并且找不出反例,这就可以考虑使用贪心,这个思考的过程其实就是我们的贪心策略
3.确定贪心策略后,就去模拟贪心的过程就可以解决问题了,通常是使用“循环”
2.动态规划
2.1动态规划概述
动态规划(Dynamic Programming,DP)是一种算法设计方法,它通过将复杂问题分解为更简单的子问题来解决。这种方法特别适用于那些具有重叠子问题和最优子结构特性的问题。
动态规划的核心在于两个主要概念:状态定义和状态转移。状态定义涉及如何描述问题的各个阶段或步骤,而状态转移则涉及如何从一个状态到达另一个状态,通常通过状态转移方程来描述3
2.2动态规划常用场景
- 最优子结构性质:如果问题的最优解所包含的子问题的解也是最优的,我们就称该问题具有最优子结构性质(即满足最优化原理)。最优子结构性质为动态规划算法解决问题提供了重要线索。
- 无后效性:即子问题的解一旦确定,就不再改变,不受在这之后、包含它的更大的问题的求解决策影响(马尔科夫性)。
- 子问题重叠性质:子问题重叠性质是指在用递归算法自顶向下对问题进行求解时,每次产生的子问题并不总是新问题,有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质,对每一个子问题只计算一次,然后将其计算结果保存在一个表格中,当再次需要计算已经计算过的子问题时,只是在表格中简单地查看一下结果,从而获得较高的效率,降低了时间复杂度(记忆化)。
在算法题中,dp常常适合于解决以下问题:
- 最优化问题:如寻找最短路径、最大利润、最小成本等。
- 计数问题:如计算不同路径的数量或组合的可能性。
- 决策问题:如资源分配、背包问题、生产计划等,需要在多个可能的选择中找到最优解。
- 序列问题:如最长公共子序列、最长递增子序列等,涉及到字符串或序列的分析。
2.3动态规划解题模板
对于求最优解的问题、总体问题可以分解为局部问题,我们常常可以使用动态规划求解,对于dp解题步骤,常常有以下步骤:
1.确定dp数组及其下标含义
2.确定递推公式
3.确定递推顺序
4.dp数组如何初始化
5.打印dp数组(debug用)
3.浅谈贪心与动态规划的关系
- 一般而言,对于二者都可以解决的问题,dp相对于贪心是一种暴力
- 贪心背后包含的“智力成本”一般大于dp,也就是说贪心以人的“思考” 换 计算机的空间和时间:
- 贪心算法对每个子问题的解决方案都做出选择,不能回退
- 动态规划则会保存以前的运算结果,并根据以前的结果对当前进行选择,有回退功能。
2.贪心经典题目
区间问题
3.动态规划经典题目
3.1体会“从整体到局部”的思考过程
3.2体会“状态转移方程”系列
(1)力扣309.买卖股票的最佳时期含冷冻期与
原题连接
在做这道题目之前,我曾经做过几道力扣股票系列的其他题目,与其他题目不同的是,这道题目增加了一个冷冻期,使得状态变得十分复杂。
一开始,我只考虑了3个状态
- 买入状态
- 卖出状态
- 冷冻期
这让我只能通过50%的测试用例。究其原因,是上述三个状态会导致状态转移发生混乱(不准确)。
如下图,具体而言,冷冻期其实将卖出状态分为了下面的两个部分,而冷冻期只能由前一个部分(今天卖出状态)转移来,而不能由保持卖出状态转移,如过将两个卖出状态合并,我们定义的状态转移方程将会存在状态转移错误,即冷冻状态也可以由保持卖出状态转移。

修改为4个状态后,这道题目成功AC了。深入思考和分析这道题目之后,我对“状态转移”四个字的理解更加深刻。代码:
class Solution {
public:
int maxProfit(vector<int>& prices) {
//1.确定dp数组及其下标含义
//dp[i][0]:买入状态
//dp[i][1]:保持卖出状态
//dp[i][2]:就在今天卖出
//dp[i][3]:冷冻期
//第i天的状态为j,持有的最大现金为dp[j]
vector<vector<int>> dp(prices.size(), vector<int>(4, 0));
//4.dp数组如何初始化
dp[0][0] = - prices[0];
//3.确定递推顺序
for(int i = 1; i < prices.size(); i++){
//2.确定递推公式
//买入状态
dp[i][0] = max(dp[i -1 ][0], max(dp[i-1][3] - prices[i], dp[i-1][1] -prices[i]));
//保持卖出状态
dp[i][1] = max(dp[i - 1][1],dp[i-1][3]);
//今天卖出
dp[i][2] = dp[i - 1][0] + prices[i];
//冷冻状态
dp[i][3] = dp[i-1][2];
//5.打印dp数组
//cout << dp[i][0] << ' ' << dp[i][1] <<' ' << dp[i][2] << ' ' << endl;
}
return max(dp[prices.size() - 1][3],max(dp[prices.size() - 1][1], dp[prices.size() - 1][2]));
}
};
(3)力扣714.买卖股票的最佳时期含手续费
这道题目我是紧随309做的,用自己的思路一次AC,但是有新的体会,我的代码:
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
//1.确定dp数组及其下标含义
//dp[i][0]:买入付费状态
//dp[i][1]:买入保持状态
//dp[i][2]:卖出状态(不持有股票)
//第i天的状态为j,最大现金为dp[i][j]
vector<vector<int>> dp(prices.size(), vector<int>(3,0));
//4.dp数组如何初始化
dp[0][0] = -prices[0] - fee;
dp[0][1] = -prices[0] - fee;
//3.确定递推公式
for(int i = 1; i < prices.size(); i++){
//2.确定递推公式
//买入付费状态
dp[i][0] = dp[i-1][2]-prices[i] - fee;
//买入保持状态
dp[i][1] = max(dp[i-1][0], dp[i-1][1]);
//卖出状态
dp[i][2] = max(max(dp[i-1][0] + prices[i], dp[i-1][1] + prices[i]), dp[i-1][2]);
//cout << dp[i][0] << ' ' << dp[i][1] <<' ' << dp[i][2] << ' ' << endl;
}
return dp[prices.size() - 1][2];
}
};
大佬的解法:
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int n = prices.size();
vector<vector<int>> dp(n, vector<int>(2, 0));
dp[0][0] -= prices[0]; // 持股票
for (int i = 1; i < n; i++) {
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);
}
return max(dp[n - 1][0], dp[n - 1][1]);
}
};
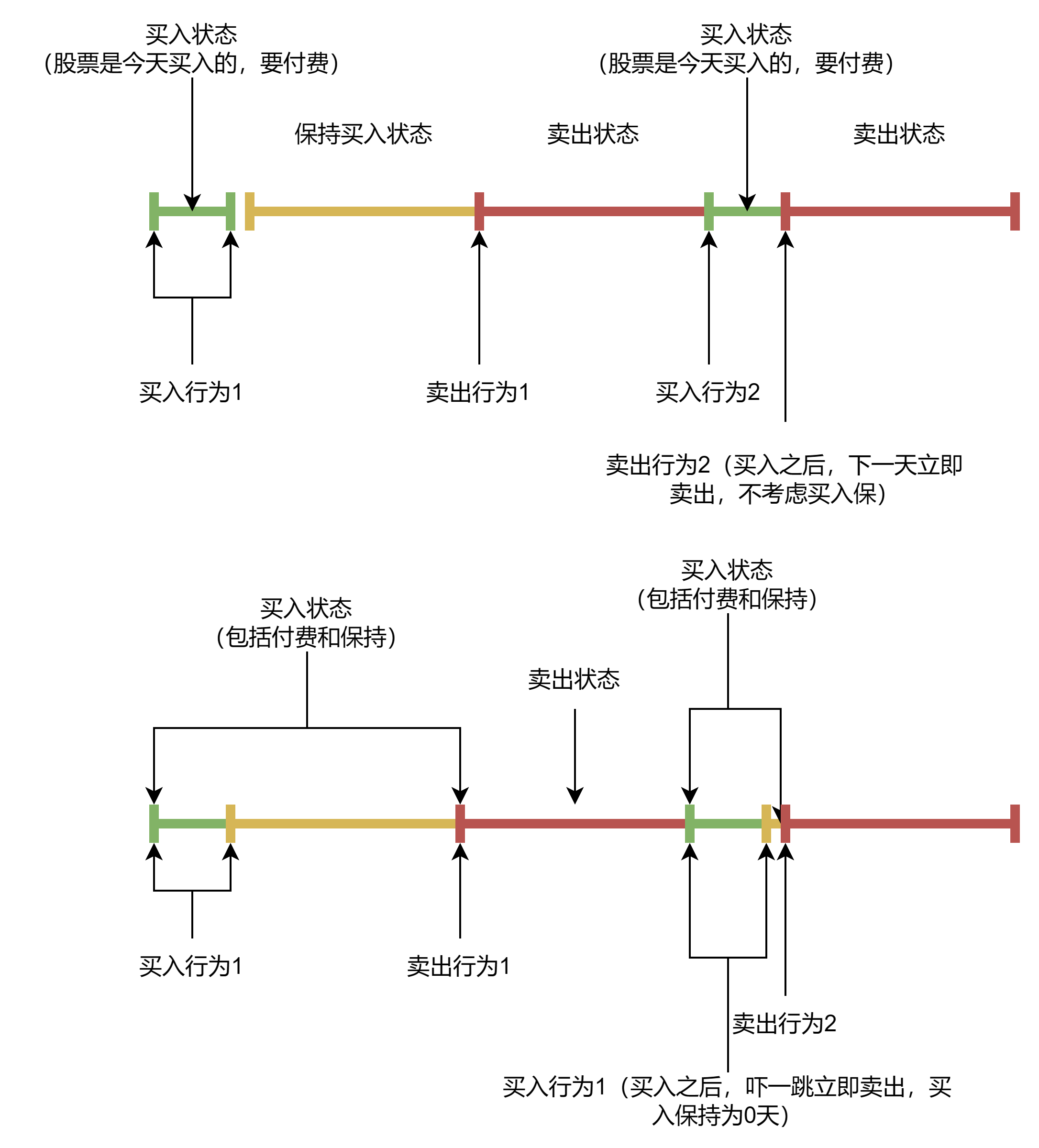
可以看到,受到上一道题冷冻期的影响,我把买入(持有)状态分为了“买入付费”和“买入保持”,但其实这两个状态是可以合并为一个状态的,因为这个付手续费行为带来的状态买入付费状态,都是由无操作或者卖出状态转移而来。
因此大佬就没有考虑,直接将我的两个买入状态合并为一个买入状态。
总而言之,定义状态的多少其实不是解体的关键,解题的关键是我们的状态不混乱、能够正确转移。如果将状态更加精细化可以帮助我们理清思路,状态转移正确,这也是可为的。
3.3 子序列问题
(1)
3.4体会什么时候用一维dp数组,什么时候使用多维dp数组
(1)力扣718.最长重复子数组
原题链接
这道题目在开始时我是有些不知道如何下手的,但当我想到只有当数组1的一个元素等于数组2的一个元素时,重复子序列的长度才能加1,
if(nums1[i] == nums2[j])
我立马就想到最直接的方法是使用二维dp,之后状态转移变得简单起来,完整代码如下:
class Solution {
public:
int findLength(vector<int>& nums1, vector<int>& nums2) {
//1.确定dp数组及其下标含义
//以下标i对应元素结尾的数组1与以下标j对应元素结尾的数组2的最长重复子数组为dp[i][j]
vector<vector<int> > dp(nums1.size(), vector<int>(nums2.size(), 0));
//4.dp数组如何初始化
//dp[1][j] = dp[0][j - 1] + 1 ---->所有dp[0][j]都需要初始化
//dp[i][1] = dp[i - 1][0] + 1 ---->所有dp[i][0]都需要初始化
bool isSame = false;
for(int j = 0; j < nums2.size(); j ++){
if(nums1[0] == nums2[j]){
dp[0][j] = 1;
isSame = true;
}
}
for(int i = 0; i < nums1.size(); i++){
if(nums1[i] == nums2[0]){
dp[i][0] = 1;
isSame = true;
}
}
//默认两个数组中可以没有相同元素
int result = 0;
//经历过初始化后,如果发现有
if(isSame) result = 1;
//3.确定递推顺序
for(int i = 1; i < nums1.size(); i++){
//2.确定递推公式
for(int j = 1; j < nums2.size(); j++){
//如果数组1的当前元素与数组2的当前元素相等,最长长度在上一个状态(数组1以i-1结尾,数组2以j-1结尾)的基础上+1
//题目隐含的着“子数组”是连续的意思,因此dp[i][j] 只能由dp[i - 1][j - 1]转移而来,而不是dp[i - 1][j]或dp[i][j - 1]
if(nums1[i] == nums2[j]) dp[i][j] = dp[i - 1][j - 1] + 1;
//cout << dp[i][j] << " ";
///收集结果
if(dp[i][j] > result) result = dp[i][j];
}
//cout << endl;
}
return result;
}
};
3.5体会“遍历顺序”
“遍历顺序”是跟着“动态转移方程来的”,我开始没有这个概念,在做完647. 回文子串,我后知后觉,代码如下:
class Solution {
public:
int countSubstrings(string s) {
//1.确定dp数组及其下标含义
//dp[i][j]表示区间【i,j】是否是回文串,0表示不是,1表示是
vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
//4.dp数组如何初始化
int result = 0;
//3.确定遍历顺序
//根据递推公式,在dp表中,dp[i+1][j-1]在dp[i][j]下方、左方从下到上,从左到右
for(int i = s.size() - 1; i >=0; i--){
for(int j = i; j < s.size(); j++){
//2.确定递推公式
//dp[i][j]由dp[i+1][j-1]推导出来
if(s[i] == s[j]){
//同一个字符或两个相邻的字符
if(j - i <= 1){
dp[i][j] = 1;
result++;
}
else{
if(dp[i+1][j-1]){
dp[i][j] = 1;
result++;
}
}
}
//如果i和j不相等,不更新dp
}
}
return result;
}
};
体会“背包问题”
树形dp
编辑距离问题
“距离”也可以理解为“操作次数”,这类问题可以进一步具体化为:
- 两字符串的最大公共子串长度(相对位置不变,不必连续)
- 两字符串的最长重复子串长度(相对位置不变,需要连续)
- 字符串1在字符串2中出现的次数(相对位置不变,不必连续)
- 编辑字符串1和字符串2使它们相同的最小操作次数(只能进行“删除”操作)
- 编辑字符串1使之成为字符串2的最小操作次数(可以进行“删除”、“增加”、“替换”操作)
4.扩展
优先级队列
大顶堆
参考资料:
- 维基百科- 贪心
- 维基百科- 动态规划
- 代码随想录
- 洛谷